数据结构与算法-算法思想-动态规划

Posted on | Edited on | In ,

原理

使用场景

一个模型：多阶段决策最优解模型，三个特征：最优解子结构，无后效性，重复子为题。

  • 多阶段决策最优解模型：即一个问题分为多个阶段，每个阶段的决策对应一组状态，我们根据这些状态寻找一组决策序列，最中获取决策序列的最优解。
  • 三个特征：
    • 最优解子结构：问题的最优解，包含子问题的最优解。也就是能通过子问题最优解找到问题的最优解
    • 无后效性：后续的问题解决方案只依赖于前一个问题的状态，而不关心他是如何推导出来的。
    • 重复子问题：不同的决策序列到达相同阶段会产生重复的状态。

空间、时间复杂度

能用动态规划解决的问题往往都是能通过回溯算法解决的，只是回溯算法的时间复杂度往往很高是指数级的O(2^n)。用动态规划这种算法往往能很大的降低是复杂度具体会变为O(nw)
空间复杂度：冬天规划因为借住了一个2维数组states[n][w+1]，所以空间复杂度是O(nw)。实际上动态规划是拿时间换空间的一个思想。

几种算法模型的区别

  • 分治：不能抽象成多阶段决策模型，而是将一个模型分成不同的部分一次解决。
  • 贪心：是动态规划的一个特殊方法，通过局部最优解推导出全局最优解，解决问题更加高效，但是也更加受限，最优子结构，无后效性，贪心选择。
  • 回溯：能用贪心、动态规划算法解决的问题几乎都能用回溯算法解决，主要是用递归方法解决问题，通过穷举所有的可能，在经过对比获取最优解，由于复杂度是指数级，试用于小数据量
  • 动态规划：上述所属多阶段决策最优解模型，有重复的子问题，无后效性，有重复子问题。

解题思路

状态转移表法

一般我们会采用二维数组来保存每一步决策的状态，如果状态较多可以采用三维四维数组，因为状态太多所以不太适合用这个方法。

方法如下：（代码和题目在下面，纪念下根据方法手撕出来的呦~）

avator

  1. 先用回溯方法实现算法
  2. 画出递归树，找到重复子问题
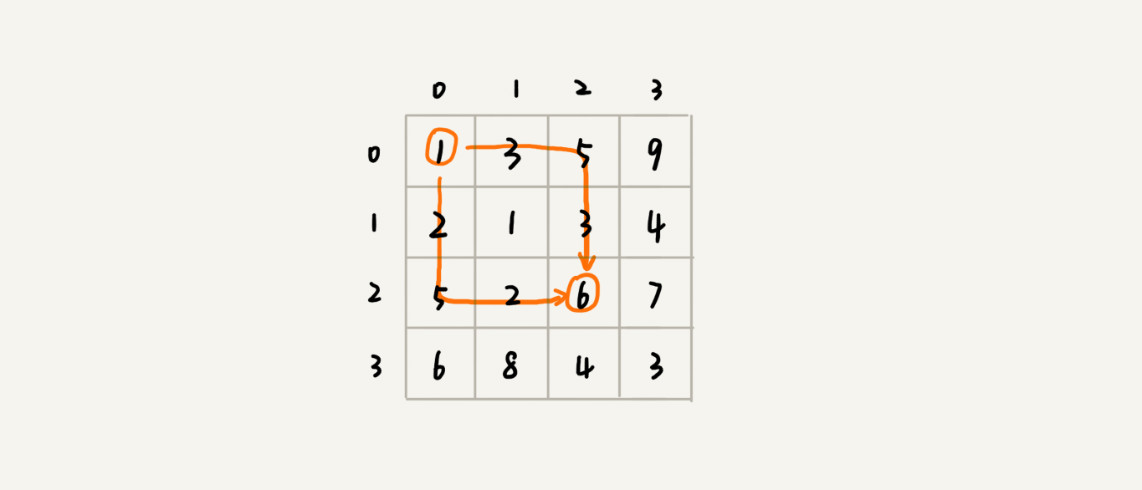
  3. 画一个状态表，往往是一个二维数组，这个二维数组分为行、列、数值。

  4. 我们根据题目要求，模拟递推我们的决策过程，来填写状态表表，这个递推的过程翻译成代码就是动态规划的过程，即状态转移表法。

    思考过程：
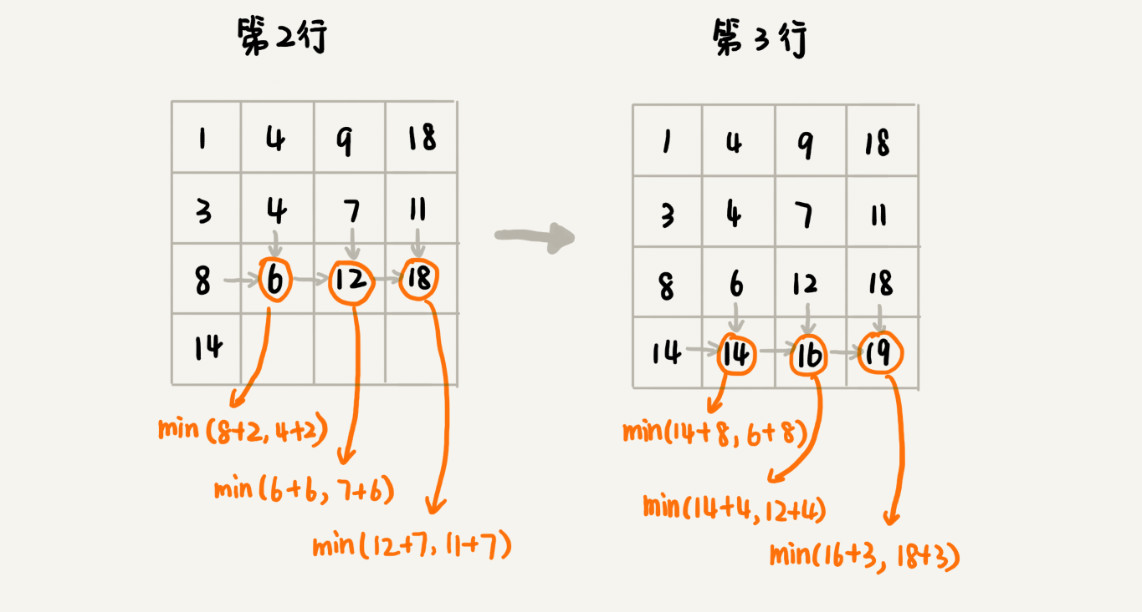
    avator

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
public class MinDist {
    private static int[][] metrix = new int[][]{{1, 3, 5, 9}, {2, 1, 3, 4}, {5, 2, 6, 7}, {6, 8, 4, 3}};

    /**
     * 示例中的动态表法：
     * 1.我们先初始化第一行和第一列的值
     * 2.根据stats[i-1][j]向下走和stats[i][j-1]向右走，找到最短距离，其他的值丢弃
     * 3.遍历stats[n-1],即最后一行找到最短距离
     *
     * @param metrix 是矩阵，
     * @return
     */
    public static int minDist(int[][] metrix) {
        int w = metrix.length;
        int h = metrix.length;
        int[][] stats = new int[w][h];

        //初始化第一行和第一列
        //第一行1，1+3，1+3+5，1+3+5+9
        //第一列1，1+2，1+2+5，1+2+5+6
        stats[0][0] = 1;
        for (int i = 1; i < w; i++) {
            stats[i][0] += stats[i - 1][0] + metrix[i][0];
        }
        for (int j = 1; j < h; j++) {
            stats[0][j] += stats[0][j - 1] + metrix[0][j];
        }

        //推导状态转移
        for (int i = 1; i < w; i++) {
            for (int j = 1; j < metrix[i].length; j++) {
                //stats[i-1][j]向下走-->stats[i - 1][j]+ metrix[i][j]
                int down = Integer.MAX_VALUE;
                if (stats[i - 1][j] > 0) {
                    down = stats[i - 1][j] + metrix[i][j];
                }

                //stats[i][j-1]向右走-->stats[i][j - 1]+ metrix[i][j]
                int right = Integer.MAX_VALUE;
                if (stats[i][j - 1] > 0) {
                    right = stats[i][j - 1] + metrix[i][j];
                }

                //找最小值
                int min = right < down ? right : down;
                if (min != Integer.MAX_VALUE) {
                    stats[i][j] = min;
                }
            }
        }

        int min = Integer.MAX_VALUE;
        for (int i = 0; i < stats[w - 1].length; i++) {
            if (stats[w - 1][i] > 0 && stats[w - 1][i] < min) {
                min = stats[w - 1][i];
            }
        }

        if (min != Integer.MAX_VALUE) {
            return min;
        }

        return -1;
    }

    public static void main(String[] args) {
        System.out.println(MinDist.minDist(metrix));
    }
}

状态转移方程

完成状态转移方程，然后将状态转移方程翻译成代码。例如上面例子，状态转移方程是

1
min_dist(i, j) = w[i][j] + min(min_dist(i, j-1), min_dist(i-1, j))

示例

0-1背包问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
/**
背包0-1问题升级版，
求解一组物体，pkg代表重量，它的价值是value，装n个物体，在w的限制下，如何使价值最大
*/
func Knapsack(pkg []int, value []int, n int, w int) int {
    //初始化state数组长队[n][w+1]
    state := make([][]int, n)
    for i := 0; i < n; i++ {
        state[i] = make([]int, w+1)
        for j := range state[i] {
            state[i][j] = -1
        }
    }

    //0元素特殊处理
    state[0][0] = 0
    if pkg[0] <= w {
        state[0][pkg[0]] = value[0]
    }

    //从第一个物体开始考察，开始状态转移
    for i := 1; i < n; i++ {
        //不放进背包中，i个物体是i-1个物体的重量j,value是state[i][j]值
        for j := 0; j < w; j++ {
            //如果上一个物体有值
            if state[i-1][j] > -1 {
                state[i][j] = state[i-1][j]
            }
        }

        //放进背包中，i个物体是i-1个物体的重量j+pkg[i],value是state[i-1][j] + value[i]
        //这里求解的是最优解，所以d当v大于当前重量的时候保留v。
        for j := 0; j < w-pkg[i]; j++ {
            if state[i-1][j] > -1 {
                v := state[i-1][j] + value[i]
                cw := j + pkg[i]
                if v > state[i][cw] {
                    state[i][cw] = v
                }
            }
        }
    }

    //遍历获取最大值
    max := -1
    for j := 0; j <= w; j++ {
        if state[n-1][j] > max {
            max = state[n-1][j]
        }
    }
    return max
}

最短路径问题

如图：

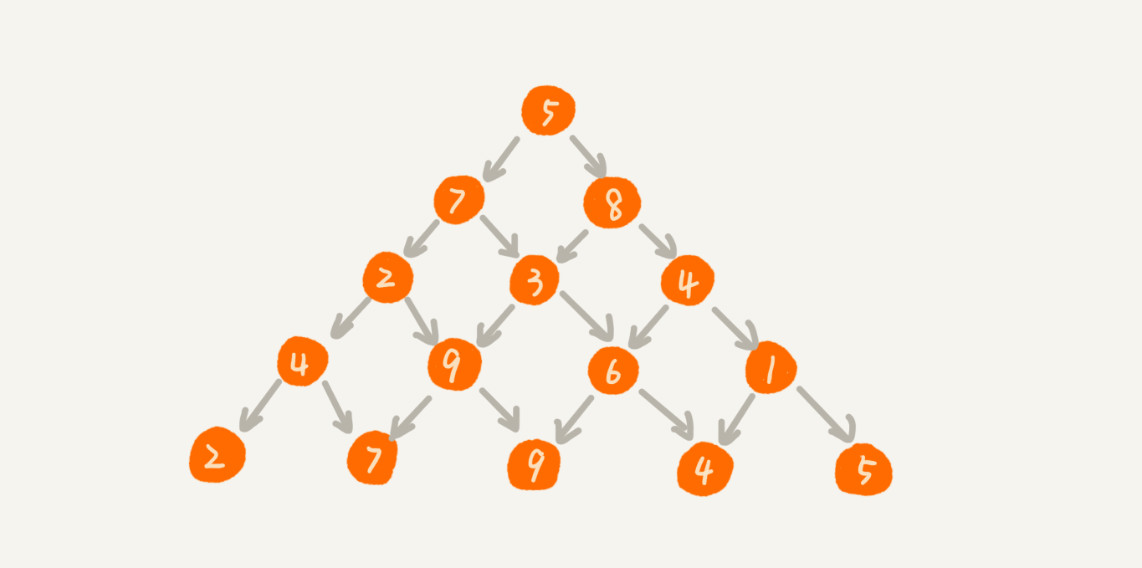
avator

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
package dp

var Triangle = [][]int{{5}, {7, 8}, {2, 3, 4}, {4, 9, 6, 1}, {2, 7, 9, 4, 5}}

/**
坐标，只能往做或者往右走，左[i-1][j]-->[i][j],右[i-1][j]-->[i][j+1]
*/
func ShortDir(arr [][]int) int {
    state := make([][]int, len(arr))
    for i := range arr {
        state[i] = make([]int, len(arr))
        for j := range state[i] {
            state[i][j] = -1
        }
    }

    n := len(arr)
    state[0][0] = arr[0][0]

    for i := 1; i < n; i++ {
        for j := 0; j < len(arr[i])-1; j++ {
            if state[i-1][j] > 0 {
                //左走
                state[i][j] = arr[i][j] + state[i-1][j]
                //右走
                state[i][j+1] = arr[i][j+1] + state[i-1][j]
            }
        }
    }

    min := int(^uint(0) >> 1)

    for j := 0; j < len(arr); j++ {
        if state[n-1][j] != -1 && state[n-1][j] < min {
            min = state[n-1][j]
        }
    }

    if min == int(^uint(0)>>1) {
        return -1
    }

    return min
}

找零问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
//纸币找零动态规划求解
func ChargeDP(money []int, sum int) int {
    //初始化状态数组 state[i][j]，纸币数，最多是sum，j是当前状态的金额
    state := make([][]bool, sum)
    for i := range state {
        state[i] = make([]bool, sum+1)
        for j := range state[i] {
            state[i][j] = false
        }
    }
    state[0][0] = true
    //min_charge(i,j)=state[i][j+max(money[0] money[1],mongey[2]])==sum-->i
    for i := 1; i < sum; i++ {
        for j := 0; j < sum; j++ {
            //从上一次状态开始推导，当前这次最大的面额然后给纸币数+1
            if state[i-1][j] {
                max := -100
                for k := 0; k < len(money); k++ {
                    //小于等于总和，然后取最大值
                    if j+money[k] <= sum && max < j+money[k] {
                        max = j + money[k]
                    }
                }
                //state[i][max]最大值获取最优解
                state[i][max] = state[i-1][j]
                if max == sum {
                    return i
                }
            }
        }
    }

    return -1
}

查找莱温斯坦距离和最大共有子串长度

todo

查找数组递增子序列

动态转移公式：
如果：array[i] < array[j]==>state[i][j] = state[i - 1][j - 1] + 1;
state[i][j] =Math.max(state[i][j - 1],state[i-1][j - 1]);

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public int getAscDP(int[] array) {
    int state[][] = new int[array.length][array.length];
    state[0][0] = 1;


    for(int j=1;j<array.length;j++){
        if(array[0]<array[j]){
            state[0][j]=2;
        }
        state[0][j]=1;
    }


    for(int i=1;i<array.length;i++){
        if(array[i]<array[0]){
            state[i][0]=2;
        }
        state[i][0]=1;
    }


    for (int i = 1; i < array.length; i++) {
        for (int j = 1; j < array.length; j++) {
            if (array[i] < array[j]) {
                state[i][j] = state[i - 1][j - 1] + 1;
            } else {
                state[i][j] =Math.max(state[i][j - 1],state[i-1][j - 1]) ;
            }
        }
    }

    return state[array.length-1][array.length-1];
}