数据结构与算法-图的广度和深度搜索

问题：接上一篇文章我们用图这种数据结构存储好友之间的关系，那么我们如何获取2度、3度关系，或者说在迷宫中如何获取出口呢？

针对上述问题介绍俩种图的搜索算法广度搜索发（bfs）、深度搜索发(dfs)

BFS-广度搜索法–2、3度人脉

如图：

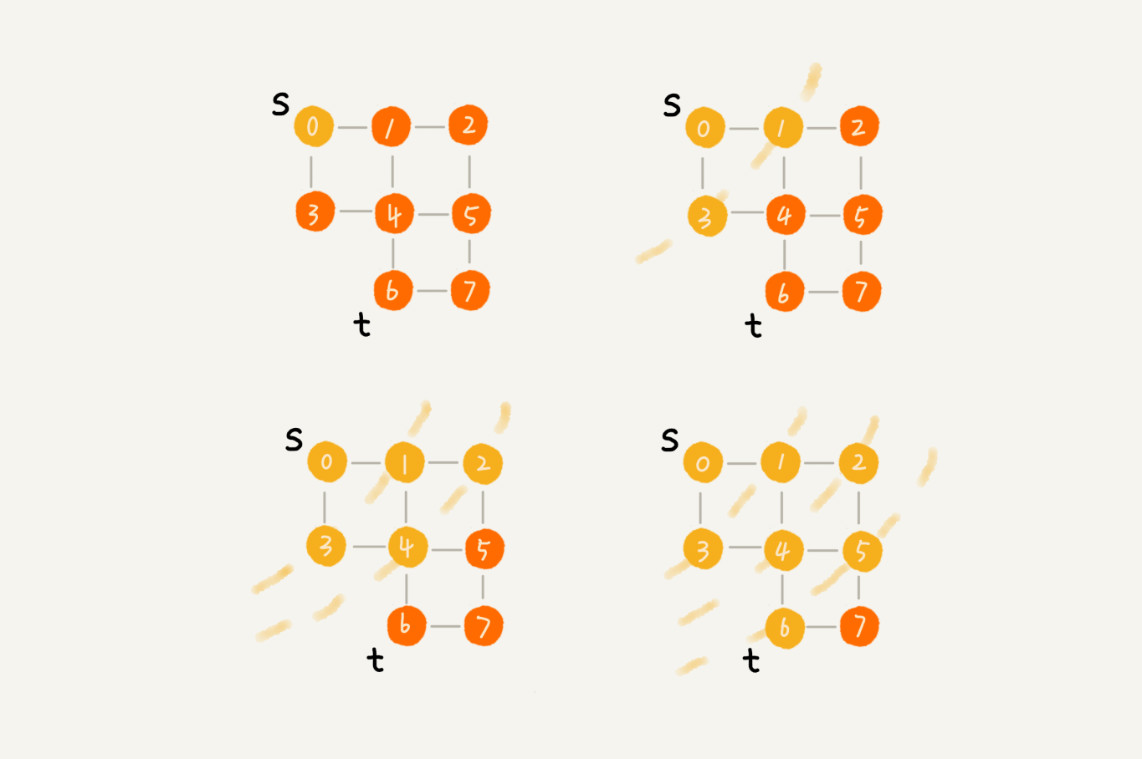
原理：我们先从起点找到最近的点，然后逐层扩大直到找到终点或者找到我们需要的层级。代码如下：

public void search(Vertex end) {
    //借用队列，将下一个要查找的点入队列
    LinkedList<Vertex> queue = new LinkedList<>();
    //记录搜索过的点，找到值后跳过
    Set<Vertex> visited = new HashSet<>();
    //记录路径key是当前的点的下标，value是来源，打印时候通过递归层层找到最开始的起点
    Map<Integer, Integer> path = new HashMap<>();

    //添加起点坐标
    queue.add(list.get(0));
    visited.add(list.get(0));
    //初始化路径
    list.forEach(v -> {
        path.put(v.getVal(), -1);
    });

    //第一层结束后才开始第二层
    while (queue.size() > 0) {
        //队列出列
        Vertex v = queue.poll();
        for (Vertex adjV : v.getAdj()) {
            if (visited.contains(adjV)) {
                continue;
            }

            //修改path和visited
            visited.add(adjV);
            path.put(adjV.getVal(), v.getVal());
            if (adjV.equals(end)) {
                //找到终点打印
                GraphUtil.printPath(path, list.get(0), end.getVal());
                return;
            }
            queue.add(adjV);
        }
    }
}

时间复杂度：E代表边，V代表点，最坏情况下访问所有的边和点，即O(V+E),可以简写为O(E)。

//上述找到N度关系
    public List<Vertex> searchByDegree(List<Vertex> list, int degree) {
      //记录当前是第几度关系的容器
      LinkedList<DegreeVertex> queue = new LinkedList<>();
      Set<Vertex> visited = new HashSet<>();

      int i = 0;
      queue.add(new DegreeVertex(i, list.get(0)));
      visited.add(list.get(0));

      List<Vertex> ret = new ArrayList<>();
      while (queue.size() > 0) {
          DegreeVertex degreeVertex = queue.poll();
          //超过度直接返回
          if (degreeVertex.getDegree() > degree) {
              break;
          }

          i = degreeVertex.getDegree() + 1;
          for (Vertex adjV : degreeVertex.vertex.getAdj()) {
              if (visited.contains(adjV)) {
                  continue;
              }

              visited.add(adjV);
              if (i == degree) {
                  ret.add(adjV);
              }
              queue.add(new DegreeVertex(i, adjV));
          }
      }

      return ret;
  }

深度优先算法

原理：类似走迷宫的场景，主要采用回溯的思想，当一条道路走不通，往回退一步选择别的道路

如图：

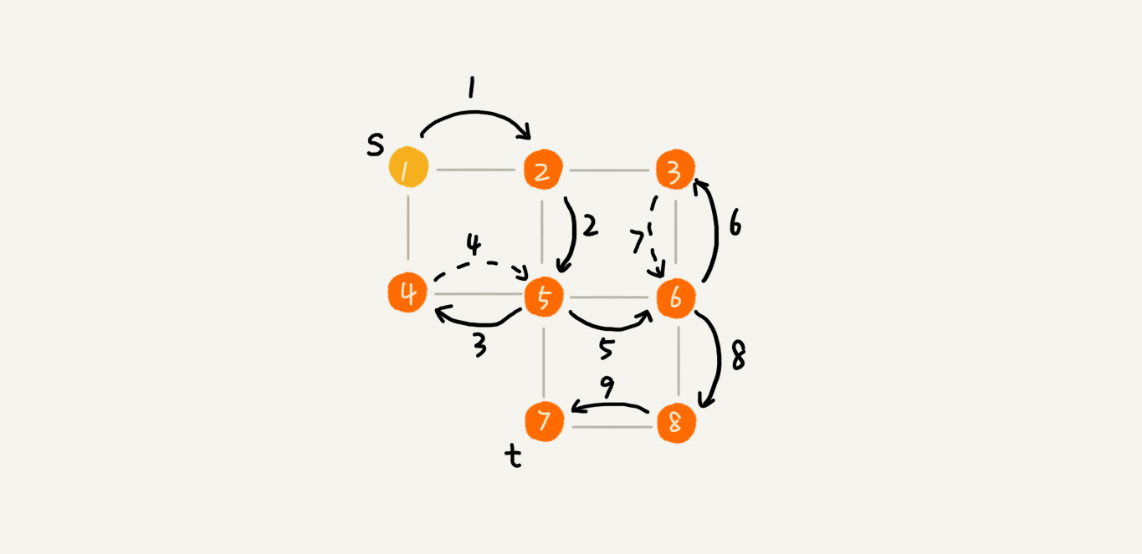
  public class DFS {

    private List<Vertex> graph = new ArrayList<>();

    //利用visited和path
    private Set<Vertex> visited = new HashSet<>();
    private Map<Integer, Integer> path = new HashMap<>();
    //用于结束递归的标记位发现后置为true停止递归
    private boolean found = false;

    public DFS(List<Vertex> graph) {
        this.graph = graph;
    }

    public void search(Vertex end) {
        graph.forEach(vertex -> {
            path.put(vertex.getVal(), -1);
        });
        search(graph.get(0), end);
        GraphUtil.printPath(path, graph.get(0), end.getVal());
    }

    public void search(Vertex start, Vertex end) {
        if (found) {
            return;
        }
        visited.add(start);
        if (start.equals(end)) {
            found = true;
            return;
        }

        for (Vertex adjV : start.getAdj()) {
            if (visited.contains(adjV)) {
                continue;
            }
            path.put(adjV.getVal(), start.getVal());
            visited.add(adjV);
            search(adjV, end);
        }
    }

}

时间复杂度，最坏情况下每个边访问俩遍所以是O(E)